在說完了神經元和神經網路後，接下來要介紹深度學習(Deep Learning, DL)了。在上篇Fig. 4-1圖中，神經網路只有三層，當中間隱藏層(Hidden Layer)增加後，人工神經網路(Artificial Neural Network, ANN)就變成深度神經網路(Deep Neural Network, DNN)了，隱藏層每一層的神經元數量代表網路的寬度，而隱藏層的層數則代表深度。當層數越多時，就越能達到深度學習的目標。

一般來說ANN或DNN在輸入層資料都是一維的，二維或多維資料也都是展開成一維資料再輸入，沒有空間概念。而層與層之間皆採用全連結方式串接神經元，故當網路寬度和深度都增加時，其權重值（或稱參數量）就會呈非線性爆增。若在一般電腦上運作時所需記憶體容量問題可能還勉強可以控制，但對於tinyML應用來說，以MCU非常有限的記憶體空間要存放網路結構、權重值（程式碼區）和計算緩衝區（隨機記憶體區）就會帶來很大的麻煩（俗稱模型塞不進去）。

為了解決這項問題，於是有學者提出採用卷積（Convolution, 或稱迴旋積）方式來共用權重值（參數量），大幅降低記憶體使用量，同時導入二（多）維空間提取特徵（濾波）概念，讓神經網路更有利於影像（灰階二維、彩色三維）類型資料的計算。其中1998年由知名學者Yann LeCun提出應用於手寫數字辨識的LeNet-5（如Fig. 5-1)就是最為知名的**卷積神經網路(Convolutional Neural Network, CNN)**代表，幾乎是每個學習DL, CNN及影像辨識的起手式。

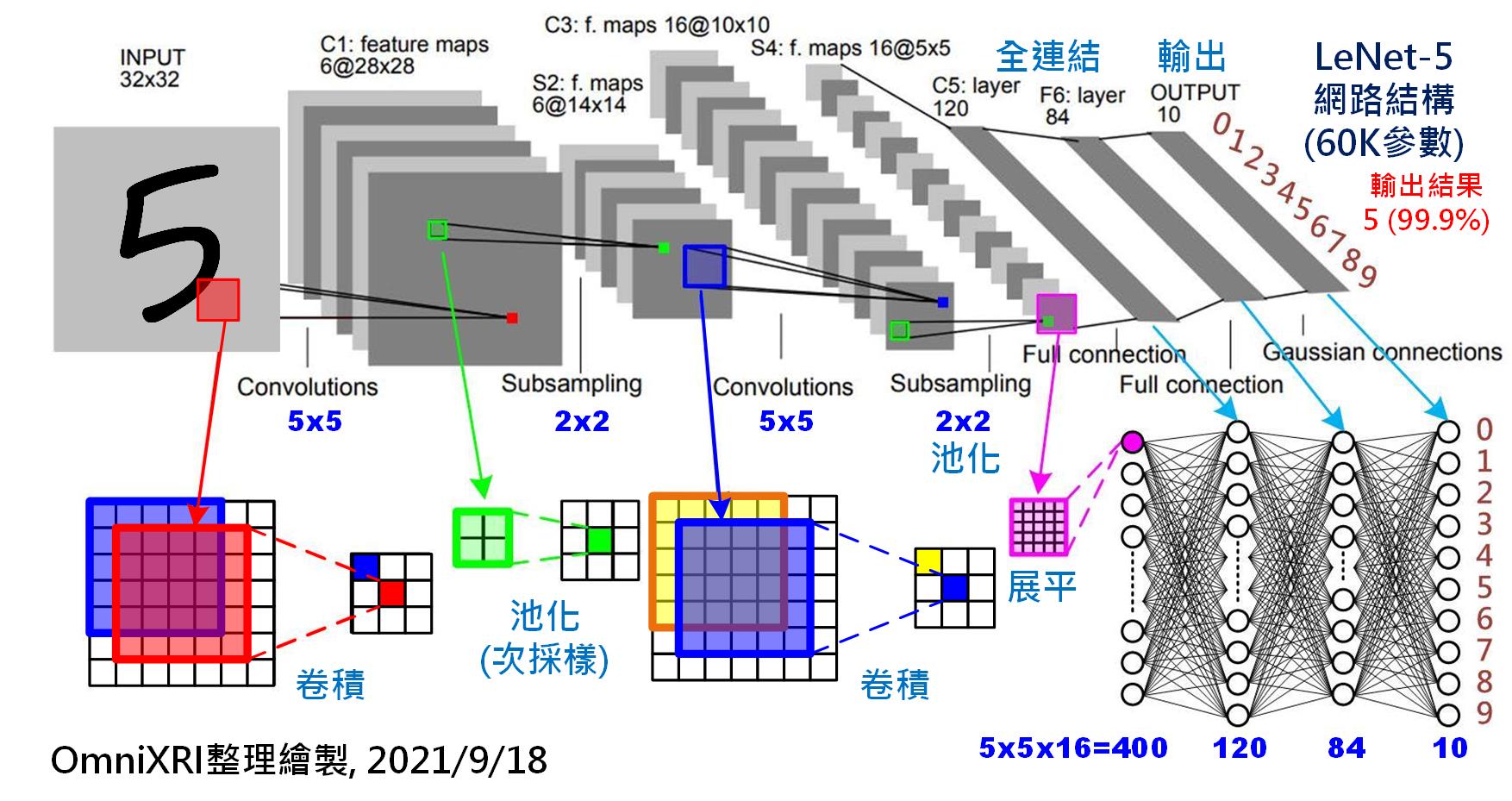
Fig. 5-1 卷積神經網路─LeNet-5。(OmniXR整理繪製, 2021/9/18)

如上圖可得知LeNet-5的完整結構，其輸入影像為一張32x32（共1024個）像素的灰階影像，首先會經過一個5x5的卷積核以步移1步的方式進行卷積，然後得到一張新的28x28像素的特徵圖(Feature Map)，這裡共使用了6個卷積核(Kernel)進行運算，所以會到6張特徵圖。換句話說只需(5x5+1)x6個參數（那個+1指的是偏置量）就夠了，但其計算量則需5x5x28x28x6(117,600)次乘加(Multiply-Accumulate, MAC)運算則已明顯暴增。為了讓運算減少，接下來使用池化(Pooling)技術將影像長寬縮小一半變成14x14像素的影像。再使用一次5x5的卷積核產生16張特徵圖並使用池化讓影像縮小到5x5。再來在進入全連結運算前，有兩種展平特徵圖的做法，一是再用一個5x5的卷積核產生120點的特徵點，另一種方式則是把16張5x5的特徵圖展平為400(5x5x16)個特徵點，再和後面120個神經元進行全連結。為更穩定輸出，這裡再加人一層有84個神經元的隱藏層。最後則是全連結到十個輸出（數字0~9)，而為了讓輸出能更明確以機率表示，通常還會加上一些正歸化函式，如Softmax等。

由於LeNet-5包含了許多DL及CNN基礎知識，接下來就一一為大家說明幾個重要元素，詳見Fig. 5-2。

• 卷積(Convolution)：要設定一個卷積核，不管是原始資料或是卷積核其內容可以是整數或是浮點數。而卷積核的大小、移步(Stride)距離會嚴重影響計算量，所以通常都會使用3x3或5x5等較小尺寸的核，而移步距離則設1或2。所謂卷積就是把原始資料乘上卷積核後所有位置加總得到的數值，這相當於在提取特定數值排列的特徵。
• 池化(Pooling)：主為目的為縮小影像，通常以長寬各縮小一半來處理，常見有最大池化和平均池化，最大池化是挑出4個點中最大值保留，而平均池化則是將4個點的值加總後再平均。前者亦有把重點特徵保留下的用意。
• 展平(Flatten)：為了能產生全連結所需的特徵點，可將較小尺寸（如3x3, 5x5）的特徵圖直接展開。由於這個動作把n維資料全部打回一維資料，因此得名。
• 全連結(Full Connected)：和[Day 04]提及的傳統神經網路相同，這裡就不多做贅述。
• 正規化Softmax函式：由於輸出有多個，但正確答案只有一個，為了強化該輸出的機率表現，所以通常還會搭配一個機率正規化函式。其中Softmax主要概念就是把所有輸出的機率加總當成分母，再以原輸出機率當成分子，求出新的機率值，這樣會更接近現實狀況。

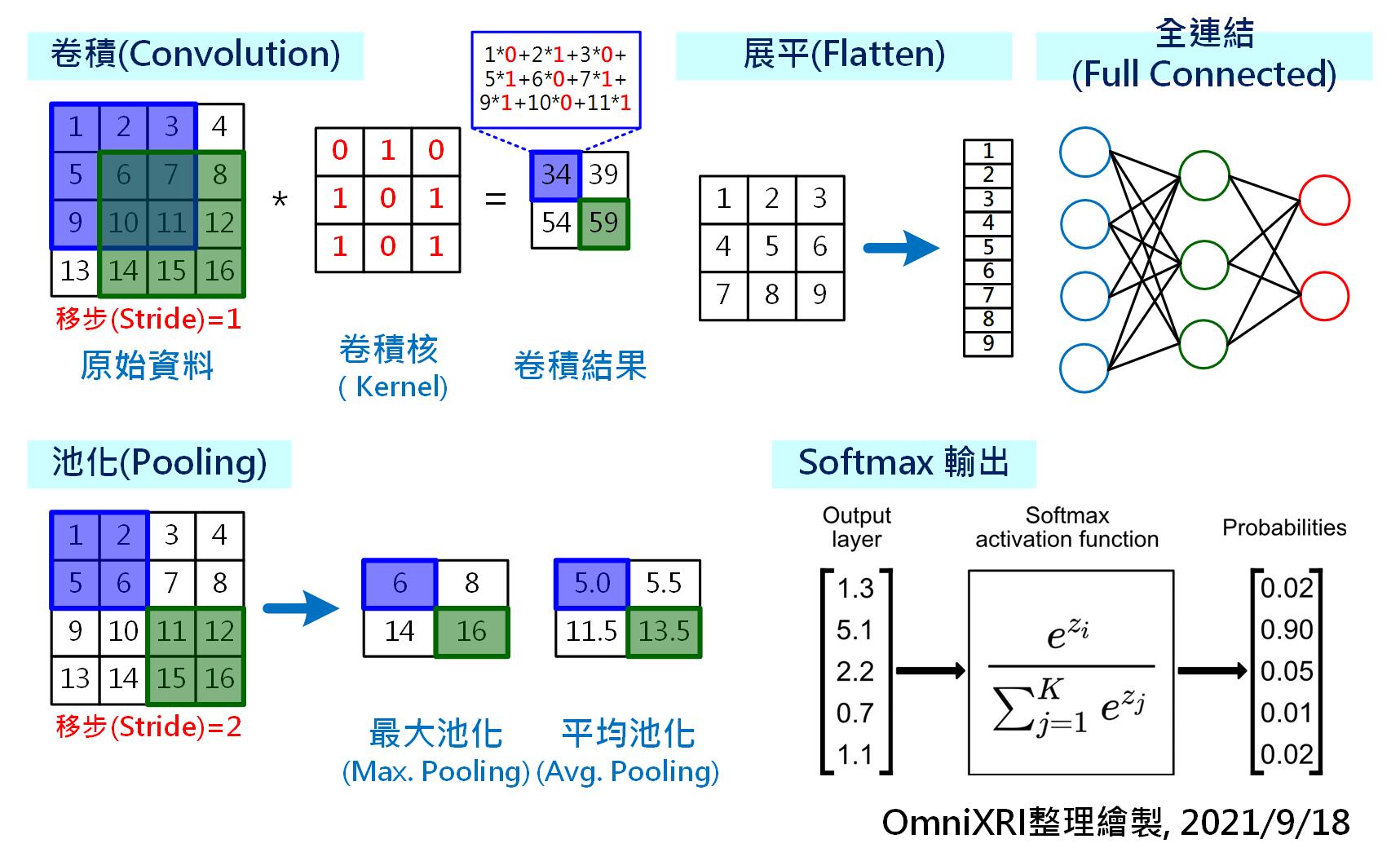
Fig. 5-2 卷積神經網路主要構成元素。(OmniXR整理繪製, 2021/9/18)

以下就用一個簡單的C語言程式來表達如何完成Fig. 5-2的卷積動作，這樣的程式可輕易在Arm Cortex-M上實現，不用CMSIS也不用Mbed，且先不考慮運行效能，也不使用平行運算指令集加速運算，只是讓大家更容易了解卷積的運作方式。

// 定義影像、卷積核大小及移步距離
#define image_w 4  // 影像寬度
#define image_h 4  // 影像高度
#define kernel_w 3 // 卷積核寬度
#define kernel_h 3 // 卷積核高度
#define stride 1   // 移步距離

void main()
{
  // 初始化影像內容
  int image[] = { 1,2,3,4,
                  5,6,7,8,
                  9,10,11,12,
                  13,14,15,16 };
  // 初始化卷積核內容
  int kernel[] = { 0,1,0,
                   1,0,1,
                   1,0,1 };    
  // 初始化卷積結果內容
  int result[] = { 0,0,
                   0,0 };
                   
  int result_w = image_w-kernel_w+1; // 卷積結果寬度為2
  int result_h = image_h-kernel_h+1; // 卷積結果高度為2 
  int result_pos; // 卷積結果儲存位置
  int kernel_pos; // 卷積核取值位置
  int image_pos;  // 影像取值位置
  
  // 計算完整卷積結果
  for(int h=0; h<result_h; h++){
    for(int w=0; w<result_w; w+=stride){
      result_pos = h*result_w+w; // 取得卷積結果儲存位置
      result[result_pos] = 0;    // 清除結果值
      
      // 計算單一卷積結果
      for(int i=0; i<kernel_h; i++){
        image_pos = (h+i)*image_w+w; // 取得影像取用位置
        kernel_pos = i*kernel_w;     // 取得卷積核取用位置
     
        for(int j=0; j<kernel_w; j++,image_pos++,kernel_pos++){
          // 將目前卷積相乘結果加總
          result[result_pos] += (image[image_pos]*kernel[kernel_pos]); 
        }
      }
      
    }
  }
}